JZ3 数组中重复的数字

描述

在一个长度为n的数组里的所有数字都在0到n-1的范围内。 数组中某些数字是重复的，但不知道有几个数字是重复的。也不知道每个数字重复几次。请找出数组中任意一个重复的数字。 例如，如果输入长度为7的数组[2,3,1,0,2,5,3]，那么对应的输出是2或者3。存在不合法的输入的话输出-1

数据范围：0≤n≤10000

进阶：时间复杂度O(n)O(n)，空间复杂度O(n)O(n)

思路1

使用Map来记录每个数出现的次数，数字的位置的计数大于1则说明是重复的。

代码1

class Solution {
public:
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param numbers int整型vector 
     * @return int整型
     */
    int duplicate(vector<int>& numbers) {
        // write code here
        map<int,int> count;
        for( int i=0; i < numbers.size(); i++) {
            count[numbers[i]]++;
            if ( count[numbers[i]] > 1) return numbers[i];
        }
        return -1;
    }
};

思路2

数据重排

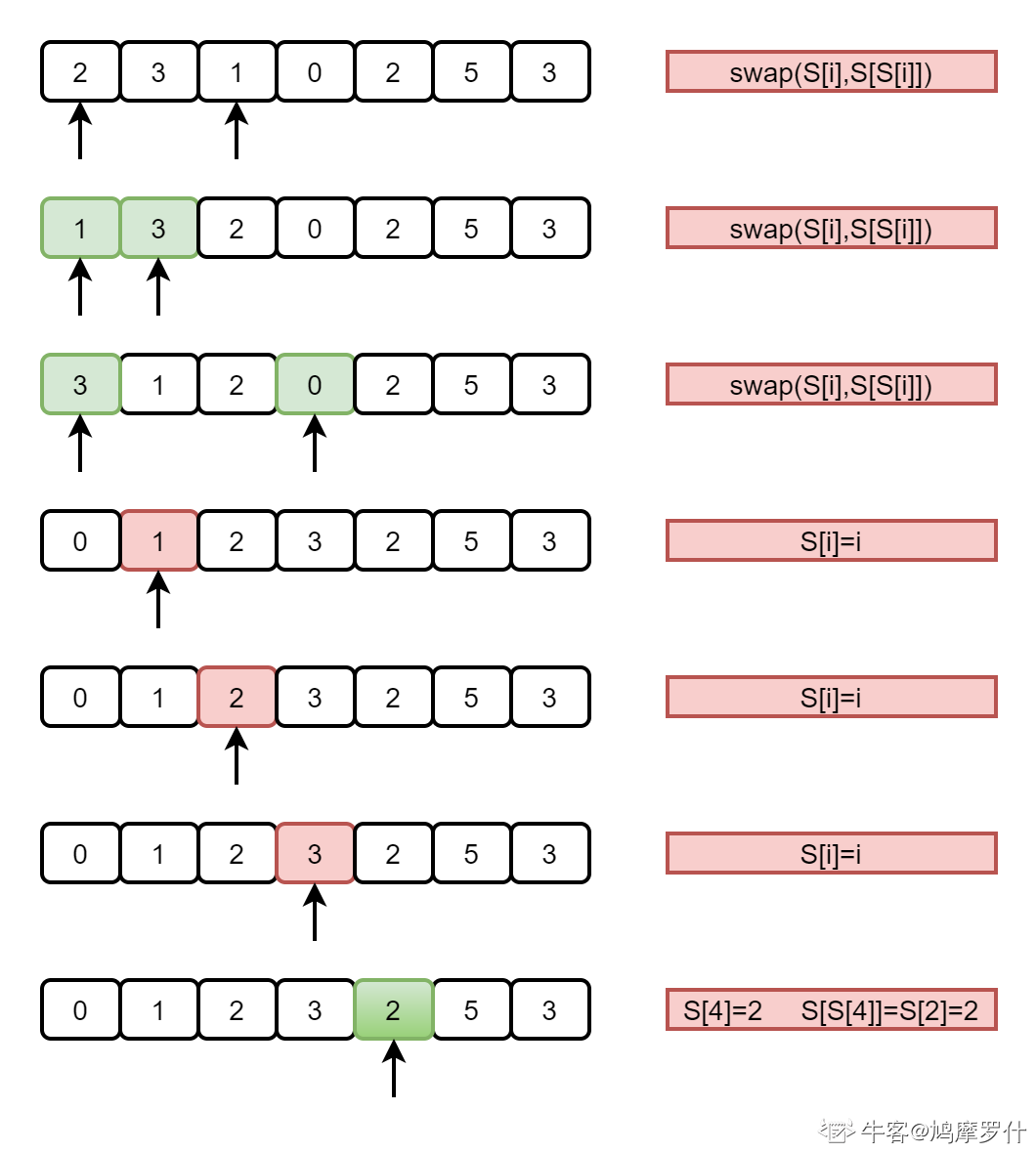
重头到尾扫描数组S中的每一个元素，当扫描到第i个元素的时候，比较第i个元素位置的值m是否等于i，如果相等，则说明该元素已经在排好序的位置，继续扫描其他元素；如果不相等，先判断m是否等于S[m]，相等则说明不同位置上的元素值相等，即元素重复。直接返回元素；否则交换m和S[m]将他们放置到排好序的位置。

仅适用于数组内数字处于0～n之间，且该方法更实用于找整个数组中只有一个不同数字的情况，多个的话可以用但是效果没有<只有一个不同数字>这种方法针对Map方法的提升大。

代码2

class Solution {
//此方法只针对数字范围是0～n-1的数组
bool duplicate(int numbers[], int length, int* duplication) {
    if(length<=0||!numbers)
        return false;
    for(int i=0;i<length;i++){
        while(numbers[i]!=i){
            if(numbers[i]==numbers[numbers[i]]){// 如果数组中第i位置的元素值A等于数组中第A位置的元素值
                *duplication = numbers[i];//这里不能用取址duplication=&numbers[i]，会出问题
                return true;
            }else{// 如果数组中第i位置的元素值A不等于数组中第A位置的元素值，则互相交换这两个位置的元素，使最后位置都对应上
                swap(numbers[i],numbers[numbers[i]]);
            }
        }
    }
    return false;
}
};

JZ51 数组中的逆序对

描述

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出。 即输出P mod 1000000007

数据范围： 对于 50% 的数据, size≤10^4
对于100% 的数据, size≤10^5

数组中所有数字的值满足 0≤val≤1000000

要求：空间复杂度 O(n)，时间复杂度 O(nlogn)

思路

看到这个题目，我们的第一反应是顺序扫描整个数组。每扫描到一个数组的时候，逐个比较该数字和它后面的数字的大小。如果后面的数字比它小，则这两个数字就组成了一个逆序对。假设数组中含有n个数字。由于每个数字都要和O(n)这个数字比较，因此这个算法的时间复杂度为O(n^2)。

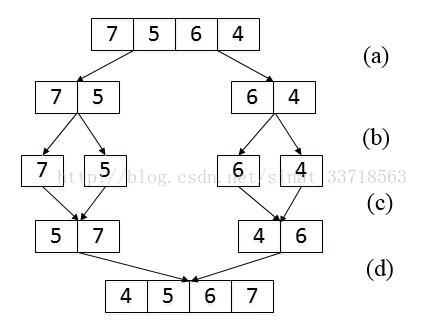
我们以数组{7,5,6,4}为例来分析统计逆序对的过程。每次扫描到一个数字的时候，我们不拿ta和后面的每一个数字作比较，否则时间复杂度就是O(n^2)，因此我们可以考虑先比较两个相邻的数字。

(a) 把长度为4的数组分解成两个长度为2的子数组；

(b) 把长度为2的数组分解成两个成都为1的子数组；

(c) 把长度为1的子数组 合并、排序并统计逆序对 ；

(d) 把长度为2的子数组合并、排序，并统计逆序对；

在上图（a）和（b）中，我们先把数组分解成两个长度为2的子数组，再把这两个子数组分别拆成两个长度为1的子数组。接下来一边合并相邻的子数组，一边统计逆序对的数目。在第一对长度为1的子数组{7}、{5}中7大于5，因此（7,5）组成一个逆序对。同样在第二对长度为1的子数组{6}、{4}中也有逆序对（6,4）。由于我们已经统计了这两对子数组内部的逆序对，因此需要把这两对子数组 排序 如上图（c）所示， 以免在以后的统计过程中再重复统计。

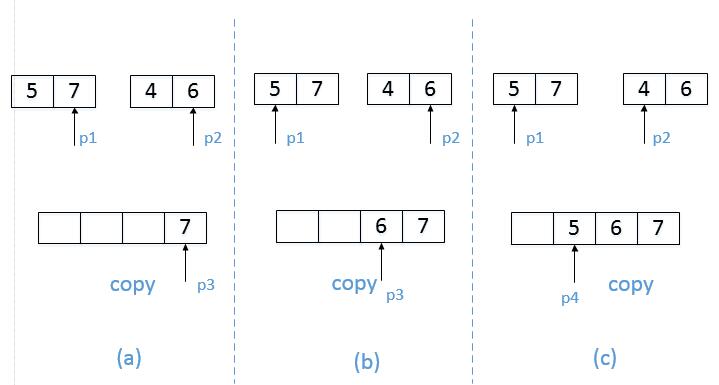
接下来我们统计两个长度为2的子数组子数组之间的逆序对。合并子数组并统计逆序对的过程如下图如下图所示。

我们先用两个指针分别指向两个子数组的末尾，并每次比较两个指针指向的数字。如果第一个子数组中的数字大于第二个数组中的数字，则构成逆序对，并且逆序对的数目等于第二个子数组中剩余数字的个数，如下图（a）和（c）所示。如果第一个数组的数字小于或等于第二个数组中的数字，则不构成逆序对，如图b所示。每一次比较的时候，我们都把较大的数字从后面往前复制到一个辅助数组中，确保 辅助数组（记为copy） 中的数字是递增排序的。在把较大的数字复制到辅助数组之后，把对应的指针向前移动一位，接下来进行下一轮比较。

过程：先把数组分割成子数组，先统计出子数组内部的逆序对的数目，然后再统计出两个相邻子数组之间的逆序对的数目。在统计逆序对的过程中，还需要对数组进行排序。如果对排序算法很熟悉，我们不难发现这个过程实际上就是归并排序

代码

class Solution {
public:
    int count;

    int InversePairs(vector<int> data) {
        if (data.size() != 0) {
            divide(data, 0, data.size() -1);
        }
        return count;
    }

    void divide(vector<int>& data, int start, int end) { // vector 记得要用引用 &
        if ( start >= end){
            return;
        }
        int mid = start + (end - start)/2; //防止溢出
        divide(data, start, mid);
        divide(data, mid+1, end);

        merge(data,start,mid,end);
    }

    void merge(vector<int>& data, int start, int mid , int end) {
        vector<int> temp(end-start+1);
        int v_size = temp.size();
        int i=start, j=mid+1, K=0;
        while( i<=mid && j<=end){
            if (data[i] <= data[j]) {
                temp[K] = data[i];
                K++;
                i++; //排序正常，从小到大，把i写入临时数组，并看下一个i++如何
            } else {
                temp[K] = data[j];
                K++;
                j++;
                count = (count + (mid - i +1)) % 1000000007; //注意此处选mid-i+1
                //后面数组的数字跳过了前面数组剩余的数字，剩余多少个就是多少的逆序对。
                //排序是从两个一组开始算的，所以之后都以mid为基准，看与i之间差多少就可以了。
            }
        }
        while ( i <= mid ) {
            temp[K++] = data[i++];
        }
        while ( j <= end ) {
            temp[K++] = data[j++];
        }
       for (int index = 0; index < temp.size(); index++) {
           data[start+index] = temp[index];
       }
    }

};

JZ40 最小的K个数

描述

给定一个长度为 n 的可能有重复值的数组，找出其中不去重的最小的 k 个数。例如数组元素是4,5,1,6,2,7,3,8这8个数字，则最小的4个数字是1,2,3,4(任意顺序皆可)。

数据范围：0≤k,n≤10000，数组中每个数的大小 0≤v*a*l≤1000

要求：空间复杂度 O(n) ，时间复杂度 O(nlogn)

思路

对数组[left, right]一次快排partition过程可得到，[left, p), p, [p+1, right)三个区间,[l,p)为小于等于p的值
[p+1,right)为大于等于p的值。
然后再判断p，利用二分法:

• 如果[left,p), p，也就是p+1个元素（因为下标从0开始），如果p+1 == k, 找到答案
• 如果p+1 < k, 说明答案在[p+1, right)区间内
• 如果p+1 > k , 说明答案在[left, p)内

代码

class Solution {
public:
    int partition(vector<int> &input,int left, int right) { // 注意对vector要用引用
        int pivot = right - 1; //注意传进来的right在此处-1最佳
        int i = left;
        for (int j = left; j < pivot; j++) {
            if ( input[j] < input[pivot] ){
                swap(input[i],input[j]);
                i++;
            }
        }
        swap(input[i],input[pivot]);
        return i;
    }
vector<int> GetLeastNumbers_Solution(vector<int> input, int k) {
    vector<int> nullRet;
    if ( k==0 || input.size() < k) {
        return nullRet;
    }
    int left = 0, right = input.size();
    while( left < right ) {
        int p = partition(input,left, right);
        if ( p + 1 == k ) {
            return vector<int>({input.begin(), input.begin()+k});
        } else if ( p + 1 < k ) {
            left = p+1;
        } else if ( p + 1 > k ) {
            right = p;
        }
    }
    return nullRet;
}
};

数据流中的中位数

描述

如何得到一个数据流中的中位数？如果从数据流中读出奇数个数值，那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值，那么中位数就是所有数值排序之后中间两个数的平均值。我们使用Insert()方法读取数据流，使用GetMedian()方法获取当前读取数据的中位数。

思路

利用优先队列来创造一个大顶堆一个小顶堆，在插入的时候就进行控制。要快速得到数据流的中位数，要保证两个优先队列长度要么相等要么差距为1.利用大顶堆队头作为标志，如果小于大顶堆队队头，就将该元素插入大顶堆当中；如果大于大顶堆队头，则将元素插入小顶堆当中。

最后小顶堆的长度只能小于或等于大顶堆，不能大于大顶堆，出现超过的情况，哪个更多，就把哪个的top插入到另一个之中。

最后按照大顶堆和小顶堆的长度来判断返回两个top除以2或者大顶堆的top

注意大顶堆（大根堆）是Top节点大于所有子节点的堆，所以是从头节点开始递减，用less关键字；

小顶堆（小根堆）则相反，Top节点小于所有子节点，从头节点开始递增，用greater关键字。

代码

#include <queue>
class Solution {
public:
    priority_queue<int, vector<int>, less<int>> p;//大顶堆
    priority_queue<int, vector<int>, greater<int>> q;//小顶堆

    void Insert(int num)
    {
        if(p.empty()||num<=p.top())
            p.push(num);
        else
            q.push(num);
        if(p.size() == q.size()+2){
            q.push(p.top());
            p.pop();
        }
        if(p.size()+1 == q.size()){
            p.push(q.top());
            q.pop();
        }
    }

    double GetMedian()
    { 
        if(p.size()==q.size())
            return (p.top()+q.top())/2.0;//注意此处一定要用2.0,不然结果是int，会把小数部分截去
        else
            return p.top();
    }
};

---