栈

JZ9 用两个栈实现一个队列

题目描述

用两个栈来实现一个队列，完成队列的Push和Pop操作。 队列中的元素为int类型。

思路

使用两个栈A、B，A是中间栈（push操作一律先插入A中），B是平时要pop的那个容器栈，当其不为空的时候pop操作一律使用B的top值，当B为空时，将A中之前push操作插入的元素全部出栈，加入B栈中。

入栈：将元素进栈A

出栈：判断栈A中元素的个数是否为1，如果等于1，则出栈，否则将栈A中的元素
出栈并放入栈B，直到栈A中的元素留下一个，然后栈A出栈，再把栈B中的元素出栈以此放入栈A中。

代码

class Solution
{
public:
    void push(int node) {
        stack1.push(node);
    }

    int pop() {
        int ret;
        if(stack2.empty()){
            while(!stack1.empty()){
                ret = stack1.top();
                stack2.push(ret);
                stack1.pop();
            }
        }

        ret = stack2.top();
        stack2.pop();
        return ret;
    }

private:
    stack<int> stack1;
    stack<int> stack2;
};

JZ30 包含min函数的栈

题目描述

定义栈的数据结构，请在该类型中实现一个能够得到栈中所含最小元素的min函数（时间复杂度应为O（1））。

注意：保证测试中不会当栈为空的时候，对栈调用pop()或者min()或者top()方法。

思路

写到时间复杂度为O（1），但是没具体要求空间复杂度，那么就可以用两个栈，辅助栈为局部最小值（比如第一个元素之间入栈，第二个元素如果小于等于第一个元素，也就是小于等于辅助栈的top，则入辅助栈）。主栈出栈的时候，判断一下当前要出栈的元素是不是辅助栈的top，如果是的话两个栈一起出栈，不是的话只针对主栈出栈。

代码

class Solution {
public:
    stack<int> minVal;
    stack<int> stackWithMin;
    void push(int value) {
        if ( stackWithMin.empty() ) {
            minVal.push(value);
        } else {
            if ( minVal.top() >= value ) { //新value小于等于辅助栈top
                minVal.push(value);
            }
        }
        stackWithMin.push(value);
    }
    void pop() {
        if( stackWithMin.top() == minVal.top() ) {
            minVal.pop();
        }

        stackWithMin.pop();
    }
    int top() {
        return stackWithMin.top();
    }
    int min() {
        return minVal.top();
    }
};

JZ73 翻转单词序列

描述

牛客最近来了一个新员工Fish，每天早晨总是会拿着一本英文杂志，写些句子在本子上。同事Cat对Fish写的内容颇感兴趣，有一天他向Fish借来翻看，但却读不懂它的意思。例如，“nowcoder. a am I”。后来才意识到，这家伙原来把句子单词的顺序翻转了，正确的句子应该是“I am a nowcoder.”。Cat对一一的翻转这些单词顺序可不在行，你能帮助他么？

数据范围：1≤n≤100
进阶：空间复杂度 O(n) ，时间复杂度 O(n) ，保证没有只包含空格的字符串

思路

使用一个string栈来存放各个单词，遇到空格就把这个单词压入栈，最后再逐个出栈，记住输出的最后一个单词之后不用加上空格。

代码

class Solution {
public:
    string ReverseSentence(string str) {
        if ( str.empty() ) {
            return str;
        }
        stack<string> reverseStack;

        bool spaceFlag = false;
        for ( int i = 0; i < str.size(); ++i) {
            if ( str[i] == ' ') {
                spaceFlag = true;
            }
        }
        if ( !spaceFlag ) return str;

        string temp ="";
        for ( int i = 0; i < str.size(); ++i) { //单词入栈
            if (str[i] != ' ') {
                temp = temp + str[i];
            }
            if ( str[i] == ' ' || i == str.size()-1) {
                reverseStack.push(temp);
                temp = "";
            }
        }

        string ret = "";
        while ( reverseStack.size() > 1 ) { //除了最后一个单词，都要带着空格入栈
            ret = ret + reverseStack.top() + " ";
            reverseStack.pop();
        }
        ret = ret + reverseStack.top(); //特殊处理最后一个单词，不用加空格
        return ret;
    }
};

JZ31 栈的压入、弹出序列

描述

输入两个整数序列，第一个序列表示栈的压入顺序，请判断第二个序列是否可能为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如序列1,2,3,4,5是某栈的压入顺序，序列4,5,3,2,1是该压栈序列对应的一个弹出序列，但4,3,5,1,2就不可能是该压栈序列的弹出序列。

1. 0<=pushV.length == popV.length <=1000

2. -1000<=pushV[i]<=1000

3. pushV 的所有数字均不相同

示例1

输入：

[1,2,3,4,5],[4,5,3,2,1]

返回值：

true

说明：

可以通过push(1)=>push(2)=>push(3)=>push(4)=>pop()=>push(5)=>pop()=>pop()=>pop()=>pop()
这样的顺序得到[4,5,3,2,1]这个序列，返回true      

示例2

输入：

[1,2,3,4,5],[4,3,5,1,2]

返回值：

false

说明：

由于是[1,2,3,4,5]的压入顺序，[4,3,5,1,2]的弹出顺序，要求4，3，5必须在1，2前压入，且1，2不能弹出，但是这样压入的顺序，1又不能在2之前弹出，所以无法形成的，返回false      

思路

使用一个真实的栈来进行模拟。在一个一个压栈的同时，对出栈序列进行头元素判定，如果相同，则能消去多少消去多少（模拟栈的头元素也要出栈），直到出栈序列的每个元素都判定过了，如果模拟栈全空了，则说明出栈序列就是真实栈的弹出序列，否则就不是。

代码

class Solution {
public:
    bool IsPopOrder(vector<int> pushV,vector<int> popV) {
        if ( pushV.empty() ) return false;
        stack<int> stackSim;
        for ( int i=0, j=0; i<pushV.size();i++ ) { //i,j设定重点
            stackSim.push(pushV[i]);
            //此处要判断stackSim是不是非空，如果空了就不能进行后面top()的调用
            while ( j<popV.size() && !stackSim.empty() && stackSim.top() == popV[j] ) {
                stackSim.pop();
                j++;
            }
        }
        return stackSim.empty();
    }
};

JZ59 滑动窗口的最大值

描述

给定一个长度为 n 的数组 nums 和滑动窗口的大小 size ，找出所有滑动窗口里数值的最大值。

例如，如果输入数组{2,3,4,2,6,2,5,1}及滑动窗口的大小3，那么一共存在6个滑动窗口，他们的最大值分别为{4,4,6,6,6,5}； 针对数组{2,3,4,2,6,2,5,1}的滑动窗口有以下6个： {[2,3,4],2,6,2,5,1}， {2,[3,4,2],6,2,5,1}， {2,3,[4,2,6],2,5,1}， {2,3,4,[2,6,2],5,1}， {2,3,4,2,[6,2,5],1}， {2,3,4,2,6,[2,5,1]}。

示例1

输入：

[2,3,4,2,6,2,5,1],3

返回值：

[4,4,6,6,6,5]

示例2

输入：

[9,10,9,-7,-3,8,2,-6],5

返回值：

[10,10,9,8]

示例3

输入：

[1,2,3,4],3

返回值：

[3,4]

思路

简单思路就是遍历每个窗口求最大值；

进阶版是维护一个单调队列（使用双端队列），这个队列队头是当前窗口最大元素的下标。注意单调队列的定义，如果入队的值大于队尾，就删掉队中比它小的所有元素直到它成为队头。然后还要考虑在滑动窗口已经滑出当前最大值所在下标的情况，这个地方也要出队。

代码

class Solution {
public:
    vector<int> maxInWindows(const vector<int>& nums, int size) {
        vector<int> ret;
        deque<int> subsequence;
        for ( int i=0; i < nums.size(); i++) {
            // 重点在双端删除，这里删的是比当前入队要小的元素
            while ( !subsequence.empty() && nums[i] > nums[subsequence.back()]) {
                subsequence.pop_back();
            }

            // 这里删的是最大但是已经不在滑动窗口的元素(删队头)
            if ( !subsequence.empty() && i - subsequence.front() > size - 1) {
                subsequence.pop_front();
            }
            subsequence.push_back(i);

            //当i>size-1即当滑动窗口成立（之前还没到size的大小）
            if ( size!=0 && i >= size -1)
                ret.push_back(nums[subsequence.front()]);
        }
        return ret;
    }
};

树

JZ55 二叉树的深度

描述

输入一棵二叉树，求该树的深度。从根结点到叶结点依次经过的结点（含根、叶结点）形成树的一条路径，最长路径的长度为树的深度，根节点的深度视为 1 。

思路

利用递归的思想，从底部开始，只要有结点，那它的高度就从0加1，之后当前结点的高度为左右子树高度的最大值加1，则该递归成型。

代码

class Solution {
public:
    int TreeDepth(TreeNode* pRoot) {
        if ( !pRoot ) {
            return 0;
        }
        int left = TreeDepth(pRoot->left);
        int right = TreeDepth(pRoot->right);
        return max(left, right) + 1;
    }
};

JZ77 按之字形顺序打印二叉树

题目描述

请实现一个函数按照之字形打印二叉树，即第一行按照从左到右的顺序打印，第二层按照从右至左的顺序打印，第三行按照从左到右的顺序打印，其他行以此类推。

思路

利用层序遍历的思想，再在每层之间遍历的时候加入一个vector用来记录当层的元素值（利用一个for循环就可以把单层的元素直接遍历完，并且把当前元素的子节点也添加进入了queue），之后在每层最后判断当前层数的奇偶性，偶数就直接调用stl里面的reverse(begin(),end())翻转vector，然后再push_back进返回的二维vector。

代码

class Solution {
public:
    vector<vector<int> > Print(TreeNode* pRoot) {
        vector<vector<int>> ret;
        queue<TreeNode*> que;
        if(!pRoot){
            return ret;
        }
        que.push(pRoot);
        bool even = false;
        while(!que.empty()){
            vector<int> vec; //注意vec位置
            int size = que.size();
            for(int i=0;i<size;i++){
                TreeNode* tem = que.front();
                que.pop();
                vec.push_back(tem->val);
                if(tem->left)
                    que.push(tem->left);
                if(tem->right)
                    que.push(tem->right);
            }
            if(even)
                std::reverse(vec.begin(),vec.end());
            ret.push_back(vec);
            even = !even;
        }
        return ret;
    }
};

JZ79 判断是不是平衡二叉树

描述

输入一棵节点数为 n 二叉树，判断该二叉树是否是平衡二叉树。

在这里，我们只需要考虑其平衡性，不需要考虑其是不是排序二叉树

平衡二叉树（Balanced Binary Tree），具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树

输入描述：

输入一棵二叉树的根节点

返回值描述：

输出一个布尔类型的值

思路

求二叉树高度的变体，每次求一个结点的高度需要求左右子树的高度，则在求左右子树高度时增加一个判断左右子树是否高度差大于1即可。

代码

class Solution {
public:
    bool result = true; //全局变量记录是否非平衡树
    int getHeight(TreeNode* pRoot) {
        if ( !pRoot ) {
            return 0;
        }
        int left = 0, right = 0;
        if ( pRoot->left) {
            left = getHeight(pRoot->left) + 1;
        }
        if ( pRoot->right ) {
            right = getHeight(pRoot->right) + 1;
        }
        if (abs(left-right)>1) { //判断左右子树是否高度差大于1
            result = false; 
        }
        return max(left,right);
    }
    bool IsBalanced_Solution(TreeNode* pRoot) {
        getHeight(pRoot);
        return result;
    }
};

JZ54 二叉搜索树的第k个节点

描述

给定一棵结点数为n 二叉搜索树，请找出其中的第 k 小的TreeNode结点值。

1.返回第k小的节点值即可

2.不能查找的情况，如二叉树为空，则返回-1，或者k大于n等等，也返回-1

3.保证n个节点的值不一样

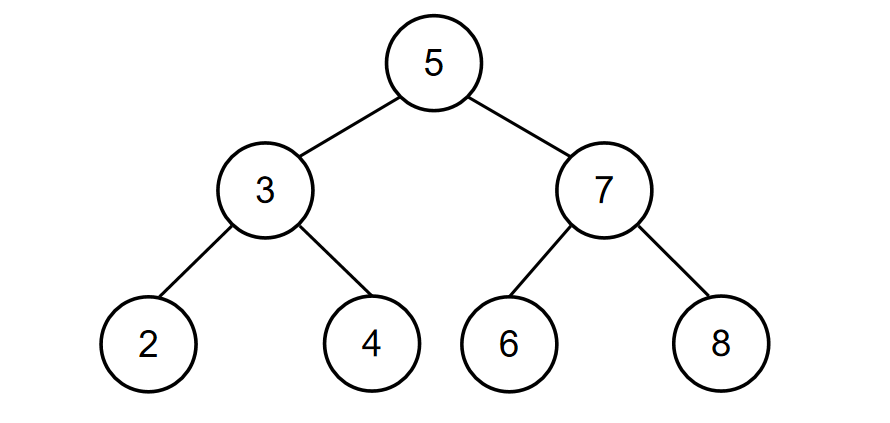
如输入{5,3,7,2,4,6,8},3时，二叉树{5,3,7,2,4,6,8}如下图所示：

该二叉树所有节点按结点值升序排列后可得[2,3,4,5,6,7,8]，所以第3个结点的结点值为4，故返回对应结点值为4的结点即可。

思路

使用中序遍历把结点值都存储到一个vector中，最后返回这个vector第k个数就可（k-1索引）；

注意考虑遍历完整个树vector大小还是没有k大的情况。

代码

class Solution {
public:
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param proot TreeNode类 
     * @param k int整型 
     * @return int整型
     */
    vector<int> result;

    int KthNode(TreeNode* proot, int k) {
        // write code here
        if (!proot) return -1;
        inOrder(proot);
        if (k == 0 || k > result.size())
            return -1;
        return result[k-1];
    }

    void inOrder(TreeNode* node) { //中序遍历，值插入vector
        if ( !node ) return;
        if (node->left)
            inOrder(node->left);
        result.push_back(node->val);
        if (node->right)
            inOrder(node->right);
    }
};

JZ82 二叉树中和为某一值的路径(一)

描述

给定一个二叉树root和一个值 sum ，判断是否有从根节点到叶子节点的节点值之和等于 sum 的路径。

1.该题路径定义为从树的根结点开始往下一直到叶子结点所经过的结点

2.叶子节点是指没有子节点的节点

3.路径只能从父节点到子节点，不能从子节点到父节点

4.总节点数目为n

5->4->11->2的结点和为22

思路

递归题，当传入的root为null时返回false，如果root没有左右子树且值为和（实际上是减完之后剩下的数值），其它情况递归到左右子树，以左右子树的结果为准。

代码

class Solution {
public:

    // 递归求解，当root为空返回false，当到达叶子节点，并且和位sum返回true
    // 其他情况递归调用左右子树

    bool hasPathSum(TreeNode* root, int sum) {
        if ( root == nullptr ) return false;
        if ( !root -> left && !root->right ) return sum == root->val;
        return hasPathSum(root->left, sum - root->val) || hasPathSum(root->right, sum - root->val);
    }
};

JZ34 二叉树中和为某一值的路径(二)

描述

输入一颗二叉树的根节点root和一个整数expectNumber，找出二叉树中结点值的和为expectNumber的所有路径。

1.该题路径定义为从树的根结点开始往下一直到叶子结点所经过的结点

2.叶子节点是指没有子节点的节点

3.路径只能从父节点到子节点，不能从子节点到父节点

4.总节点数目为n

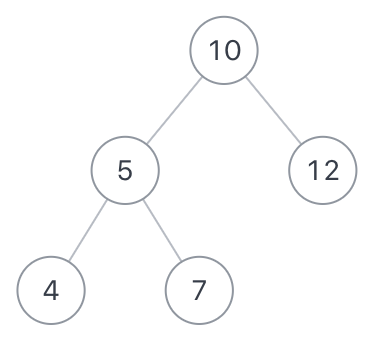
如二叉树root为{10,5,12,4,7},expectNumber为22

则合法路径有[[10,5,7],[10,12]]

思路

DFS + 回溯的思路，设立一个全局变量vector 保存当前DFS搜索到的路径，每次新到一个非空node都将该node的val存入vector，如果该路径和就为我们想要的值，则把这个vector存入最终返回的结果中，如果不相等且没有子节点了，则回溯，弹出vector尾部val。

关键点：

回溯相当于后序遍历，是在递归完左右子树之后才pop_back()的。

代码

class Solution {
public:
    vector<int> nums;
    vector<vector<int>> res;
    void dfs(TreeNode* node, int num) {
        if ( node == nullptr ) {
            return;
        }
        nums.push_back(node->val);
        if ( !node->left && !node->right && node->val == num) {
            res.push_back(nums); //找到了想要的路径，将nums push_back进res
        }
        if(node->left) {
            dfs(node->left,num - node->val);
        }
        if(node->right) {
            dfs(node->right,num - node->val);
        }
        nums.pop_back(); //回溯
    }
    vector<vector<int>> FindPath(TreeNode* root,int expectNumber) {
        dfs(root, expectNumber);
        return res;
    }
};

JZ68 二叉搜索树的最近公共祖先

描述

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

1.对于该题的最近的公共祖先定义:对于有根树T的两个节点p、q，最近公共祖先LCA(T,p,q)表示一个节点x，满足x是p和q的祖先且x的深度尽可能大。在这里，一个节点也可以是它自己的祖先.

2.二叉搜索树是若它的左子树不空，则左子树上所有节点的值均小于它的根节点的值； 若它的右子树不空，则右子树上所有节点的值均大于它的根节点的值

3.所有节点的值都是唯一的。

4.p、q 为不同节点且均存在于给定的二叉搜索树中。

数据范围:

3<=节点总数<=10000

0<=节点值<=10000

思路

由于搜索二叉树的定义，我们可以知道往下搜索的时候，要么搜到p、q两点的祖先，要么搜到比p、q两点都大或者比p、q两点都小的结点。

这样当我们搜到第一个处于p、q两点数值区间内的结点，即为其共同祖先。

代码

class Solution {
public:
    int lowestCommonAncestor(TreeNode* root, int p, int q) {
        // write code here
        if ( root->val < p && root->val < q ) {
            return lowestCommonAncestor(root->right,p,q);
        }
        else if ( root->val > p && root->val > q ) {
            return lowestCommonAncestor(root->left,p,q);
        }
        return root->val;
    }
};

JZ86 在二叉树中找到两个节点的最近公共祖先

描述

给定一棵二叉树(保证非空)以及这棵树上的两个节点对应的val值 o1 和 o2，请找到 o1 和 o2 的最近公共祖先节点。

数据范围：树上节点数满足 1≤n≤10^5 , 节点值val满足区间 [0,n)

要求：时间复杂度 O(n)

注：本题保证二叉树中每个节点的val值均不相同。

如当输入{3,5,1,6,2,0,8,#,#,7,4},5,1时，二叉树{3,5,1,6,2,0,8,#,#,7,4}如下图所示：

所以节点值为5和节点值为1的节点的最近公共祖先节点的节点值为3，所以对应的输出为3。

节点本身可以视为自己的祖先

思路

根据以上定义，若 root 是p,q 的 最近公共祖先 ，则只可能为以下情况之一：

1. p 和 q 在root 的子树中，且分列 root 的 异侧（即分别在左、右子树中）；
2. p=root ，且 q 在 root 的左或右子树中；
3. q=root ，且 p 在 root 的左或右子树中；

考虑通过递归对二叉树进行先序遍历 (赋值为先序，回溯判断为后序)，当遇到节点 p 或 q 时返回。从底至顶回溯，当节点 p,q 在节点 root 的异侧时，节点 root 即为最近公共祖先，则向上返回 root 。

终止条件：

1. 当越过叶节点，则直接返回 null ；
2. 当 root 等于 p,q ，则直接返回 root ；

递推工作：

1. 开启递归左子节点，返回值记为 left ；
2. 开启递归右子节点，返回值记为 right ；

返回值：

根据 left 和 right ，可展开为四种情况；

1. 当 left 和 right 同时为空 ：说明 root 的左 / 右子树中都不包含 p,q ，返回 null ；
2. 当 left 和 right 同时不为空 ：说明 p,q 分列在 root 的 异侧 （分别在 左 / 右子树），因此 root 为最近公共祖先，返回 root ；
3. 当 left 为空 ，right 不为空 ：p,q 都不在 root 的左子树中，直接返回 right （此时right代表是right这边的）。
4. 当 left不为空 ， right 为空 ：与情况 3. 同理；

代码

class Solution {
public:

    TreeNode *dfsRecursive( TreeNode* root, int o1, int o2 ){
        if ( !root || root->val == o1 || root->val == o2 ) {
            return root;
        }
        TreeNode *left = dfsRecursive(root->left, o1, o2);
        TreeNode *right = dfsRecursive(root->right, o1, o2);
        if ( left && right ) return root;
        if ( !left && right ) return right; // 注意这里是返回右子树的结果，不是单纯一个结点
        if ( !right && left ) return left; // 同理，返回左子树的结果
        return NULL;
    }


    int lowestCommonAncestor(TreeNode* root, int o1, int o2) {
        return dfsRecursive(root, o1, o2)->val;
    }
};

JZ29 顺时针打印矩阵

JZ38 字符串的排列

---