45. 跳跃游戏 II
描述
给你一个非负整数数组 nums ,你最初位于数组的第一个位置。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
你的目标是使用最少的跳跃次数到达数组的最后一个位置。
假设你总是可以到达数组的最后一个位置。
示例 1:
输入: nums = [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
从下标为 0 跳到下标为 1 的位置,跳 1 步,然后跳 3 步到达数组的最后一个位置。
示例 2:
输入: nums = [2,3,0,1,4]
输出: 2
提示:
1 <= nums.length <= 104
0 <= nums[i] <= 1000
思路
贪心思想,一直记录在某个阶段中能够达到的最远距离。
我们需要遍历整个数组,在遍历的同时,记录下当前阶段中能走最远距离在哪。在到达这个最远距离之前,这个阶段都算作为一步之内。
维护当前能够到达的最大下标位置,记为边界。我们从左到右遍历数组,到达边界时,更新边界(到这个阶段能走到的最远距离)并将跳跃次数增加 1。
最终最远距离大于等于数组长度减一时,说明我们step数量足够了(此时step也要加一)。
代码
class Solution {
public:
int jump(vector<int>& nums) {
int end = 0, current = 0, n = nums.size()-1;
int step = 0, maxPos = 0;
while ( end < n ) {
maxPos = max(maxPos, current + nums[current]); //每次都看看在当前位置下能走的最远值能不能更新
if ( current == end) { //到达边界
end = maxPos;
step++;
}
current++;
}
return step;
}
};23. Merge k Sorted Lists
描述
You are given an array of k linked-lists lists, each linked-list is sorted in ascending order.
Merge all the linked-lists into one sorted linked-list and return it.
- Example 1:
Input: lists = [[1,4,5],[1,3,4],[2,6]]
Output: [1,1,2,3,4,4,5,6]
Explanation: The linked-lists are:
[
1->4->5,
1->3->4,
2->6
]
merging them into one sorted list:
1->1->2->3->4->4->5->6
- Example 2:
Input: lists = []
Output: []
- Example 3:
Input: lists = [[]]
Output: []
思路
用容量为K的最小堆优先队列,把链表的头结点都放进去,然后出队当前优先队列中最小的,挂上链表,然后让出队的那个节点的下一个入队,再出队当前优先队列中最小的,直到优先队列为空。
其中需要注意的是如何写priority_queue的比较函数:使用struct,重载()运算符,在重载里面写bool函数。
代码
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
struct cmp {
bool operator() (ListNode* node1, ListNode *node2) {
return node1->val > node2->val ? true:false;
}
};
ListNode* mergeKLists(vector<ListNode*>& lists) {
if ( lists.empty() ) {
return nullptr;
}
ListNode *preHead = new ListNode(0);
ListNode *current = preHead;
priority_queue<ListNode*, vector<ListNode*>, cmp> pq;
for (ListNode* list : lists) { //遍历ListNode数组(实际上就是一个包含3个ListNode头指针的数组
if ( !list ) {
continue;
}
pq.push(list);
}
while ( !pq.empty() ) {
ListNode* nextNode = pq.top();
pq.pop();
current->next = nextNode;
current = current->next;
if ( nextNode->next ) {
pq.push(nextNode->next);
}
}
return preHead->next;
}
};221. Maximal Square
描述
Given an
m x nbinarymatrixfilled with0‘s and1‘s, find the largest square containing only1‘s and return its area.
Example 1:
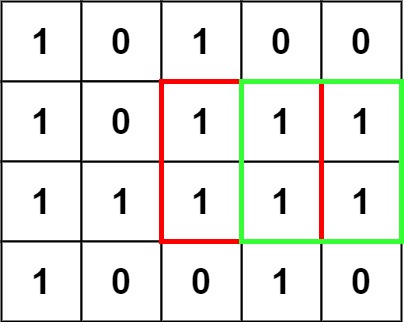
Input: matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
Output: 4Example 2:
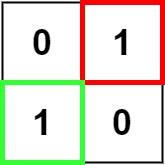
Input: matrix = [["0","1"],["1","0"]]
Output: 1Example 3:
Input: matrix = [["0"]]
Output: 0思路
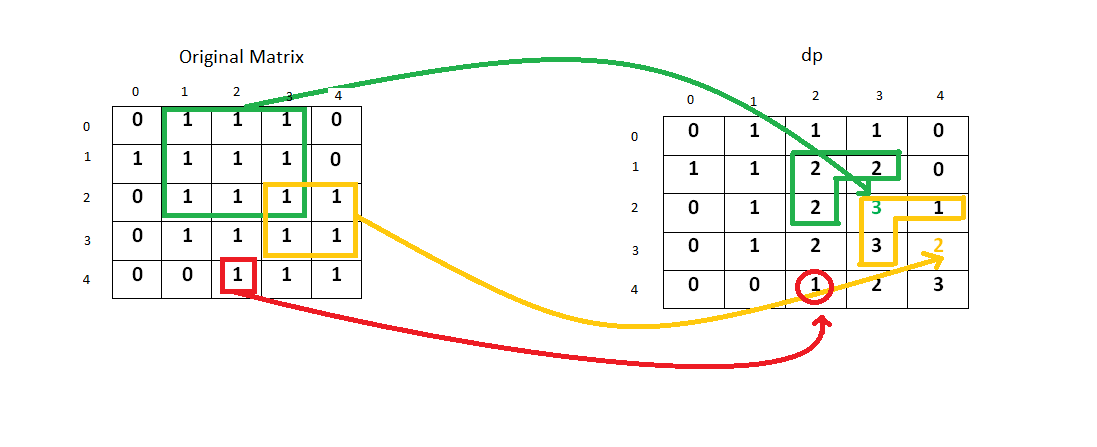
动态规划题,我们用动态规划矩阵做。
首先我们的状态转移方程的输入输出大小是固定的,而在现在这个算最大正方形里面,我们最好的方式就是2x2子矩阵。右下角为输出,左上三个元素值为输入。
首先边界:
即 i=0 或者 j=0 的时候不存在大于1的正方形,则此处正方形大小就等于它元素值(注意要从string转为int)。
之后就是用左上三个
dp[][]值来求右下角的dp[][],取左上中最小的值(即以该点为右下角,最大的正方形边长是多少)加一:指当前新的正方形最大边长为多少。状态转移方程为:
dp[i][j] = min(dp[i-1][j-1],min(dp[i][j-1],dp[i-1][j])) + 1;
代码
//主要理解的是dp数组记录的是以该位置为右下角组成的正方形,边长有多大
class Solution {
public:
int maximalSquare(vector<vector<char>>& matrix) {
if(matrix.empty()){
return 0;
}
int m = matrix.size(),n = matrix[0].size();
vector<vector<int>> dp(m,vector(n,0));
int res = INT_MIN;
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
if(i==0||j==0||matrix[i][j]=='0'){
dp[i][j] = matrix[i][j] - '0';
//注意这里是-'0'而不是赋值为0,指的是初始化的时候是啥就是啥边长
}
else{
dp[i][j] = min(dp[i-1][j-1],min(dp[i][j-1],dp[i-1][j])) + 1;
//2x2矩阵,[i,j]为右下角的,其值为左上3个的最小值+1
}
res = max(dp[i][j],res);
}
}
return res * res;
}
};695. Max Area of Island
描述
You are given an
m x nbinary matrixgrid. An island is a group of1‘s (representing land) connected 4-directionally (horizontal or vertical.) You may assume all four edges of the grid are surrounded by water.The area of an island is the number of cells with a value
1in the island.Return the maximum area of an island in
grid. If there is no island, return0.
Example 1:
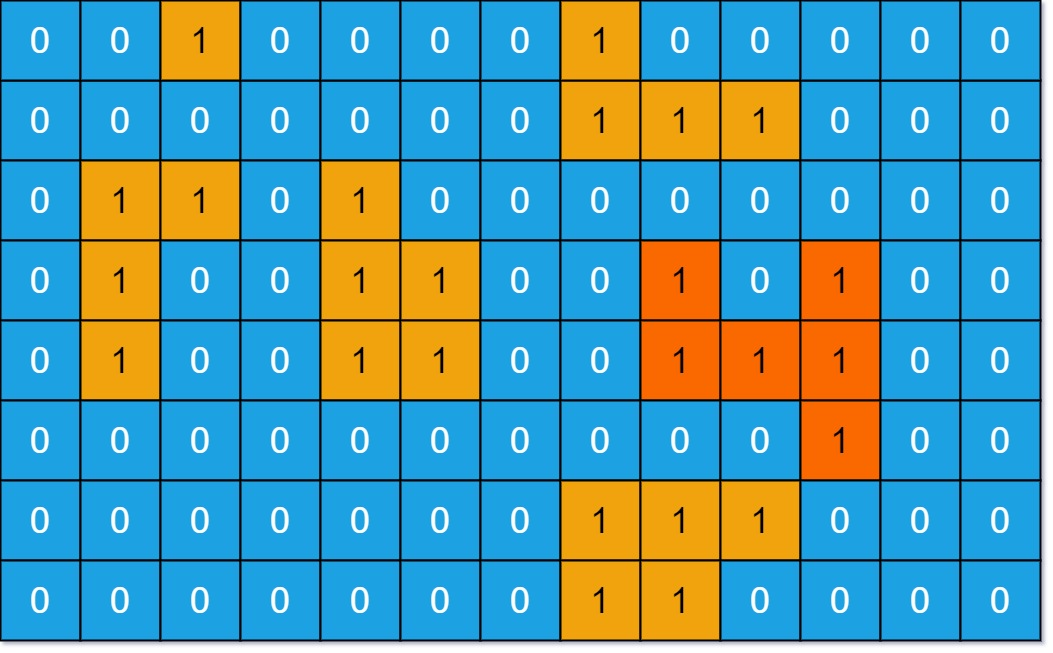
Input: grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
Output: 6
Explanation: The answer is not 11, because the island must be connected 4-directionally.Example 2:
Input: grid = [[0,0,0,0,0,0,0,0]]
Output: 0思路
像是单个岛屿在
dfs下沉没的原理。首先找到一个为1的方格,将其值从1变为0(避免二次遍历到)且这个岛屿的大小+1(递归方法加),之后对它的上下左右都dfs(指
1+dfs(...))。然后对每个格子都用dfs遍历,比对得到的maxArea大小就行。
代码
class Solution {
public:
int maxAreaOfIsland(vector<vector<int>>& grid) {
int row = grid.size();
if(row==0)
return 0;
int col = grid[0].size();
int maxarea = 0;
for(int i=0;i<row;i++){
for(int j=0;j<col;j++){
if(grid[i][j]==1){
maxarea = max(maxarea, dfs(grid,i,j,row,col));
}
}
}
return maxarea;
}
int dfs(vector<vector<int>>& grid, int i, int j, int row, int col){
if(i<0 || i>=row || j<0 || j>=col || grid[i][j]!=1){
return 0;
}
else{
grid[i][j]=0; //把当前位置设为0,然后往四周扩散,保证每个为1的点只记录一次
return 1 + dfs(grid,i+1,j,row,col)
+dfs(grid,i-1,j,row,col)
+dfs(grid,i,j+1,row,col)
+dfs(grid,i,j-1,row,col);
}
}
};200. Number of Islands
描述
Given an
m x n2D binary gridgridwhich represents a map of'1's (land) and'0's (water), return the number of islands.An island is surrounded by water and is formed by connecting adjacent lands horizontally or vertically. You may assume all four edges of the grid are all surrounded by water.
Example 1:
Input: grid = [
["1","1","1","1","0"],
["1","1","0","1","0"],
["1","1","0","0","0"],
["0","0","0","0","0"]
]
Output: 1Example 2:
Input: grid = [
["1","1","0","0","0"],
["1","1","0","0","0"],
["0","0","1","0","0"],
["0","0","0","1","1"]
]
Output: 3思路
与上一题Max Area of Island方法类似但是有所不同。
Max Area of Island是找到一个为1的方格就以此为基准累加整个岛屿的大小;本题是找到一个为1的方格就以此为基准发散沉没整个岛,找到这个1的时候整个岛屿数量加1即可。
代码
class Solution {
public:
int numIslands(vector<vector<char>>& grid) {
if(grid.size()==0)
return 0;
int row = grid.size();
int col = grid[0].size();
int count = 0;
for(int i=0;i<row;i++){
for(int j=0;j<col;j++){
if(grid[i][j]=='1'){
count++; //找到1的时候岛屿数量+1
infect(grid,i,j,row,col); //沉没整个岛屿
}
}
}
return count;
}
void infect(vector<vector<char>>& grid, int i,int j, int row, int col){
if(i<0||i>=row||j<0||j>=col||grid[i][j]!='1')//注意最重要的是grid[i][j]!='1'
return;
grid[i][j] = '0';
infect(grid,i-1,j,row,col);
infect(grid,i+1,j,row,col);
infect(grid,i,j-1,row,col);
infect(grid,i,j+1,row,col);
}
};123. Best Time to Buy and Sell Stock III
描述
You are given an array
priceswhereprices[i]is the price of a given stock on theithday.Find the maximum profit you can achieve. You may complete at most two transactions.
Note: You may not engage in multiple transactions simultaneously (i.e., you must sell the stock before you buy again).
Example 1:
Input: prices = [3,3,5,0,0,3,1,4]
Output: 6
Explanation: Buy on day 4 (price = 0) and sell on day 6 (price = 3), profit = 3-0 = 3.
Then buy on day 7 (price = 1) and sell on day 8 (price = 4), profit = 4-1 = 3.Example 2:
Input: prices = [1,2,3,4,5]
Output: 4
Explanation: Buy on day 1 (price = 1) and sell on day 5 (price = 5), profit = 5-1 = 4.
Note that you cannot buy on day 1, buy on day 2 and sell them later, as you are engaging multiple transactions at the same time. You must sell before buying again.Example 3:
Input: prices = [7,6,4,3,1]
Output: 0
Explanation: In this case, no transaction is done, i.e. max profit = 0.思路
买卖股票与之前的相关,对之后的没有影响,动态规划题。
寻找状态转移方程:
dp[k, i] = max(dp[k, i-1], prices[i] - prices[j] + dp[k-1, j-1]), j=[0..i-1]
k为第几次买卖,i为第几天卖出,j为第几天买入。如果我们不卖出,则当前的profit等于上一天的profit;
如果我们卖出(在
j天买入的股票),则当前的profit为prices[i] - prices[j] + dp[k-1, j-1]
代码
public int MaxProfitDp(int[] prices) {
if (prices.Length == 0) return 0;
var dp = new int[3, prices.Length];
for (int k = 1; k <= 2; k++) {
for (int i = 1; i < prices.Length; i++) {
int min = prices[0];
for (int j = 1; j <= i; j++)
min = min(min, prices[j] - dp[k-1, j-1]);
dp[k, i] = max(dp[k, i-1], prices[i] - min);
}
}
return dp[2, prices.Length - 1];
}7. Reverse Integer
描述
Given a signed 32-bit integer
x, returnxwith its digits reversed. If reversingxcauses the value to go outside the signed 32-bit integer range[-2^31, 2^31 - 1], then return0.
思路
翻转数字问题,需要考虑符号和大于INT_MAX的情况,则选择long为储存结果的变量。
关键语句:
res = res*10 + x%10;
代码
class Solution {
public:
int reverse(int x) {
long y = 0;
int sign = x > 0 ? 1:-1; // 符号判断
x = abs(x);
while ( x > 0) {
y = y*10 + x%10; //关键
x = x/10;
}
if ( y > INT_MAX) {
return 0;
}
return sign*y;
}
};6. Zigzag Conversion
描述
The string
"PAYPALISHIRING"is written in a zigzag pattern on a given number of rows like this: (you may want to display this pattern in a fixed font for better legibility)P A H N A P L S I I G Y I RAnd then read line by line:
"PAHNAPLSIIGYIR"Write the code that will take a string and make this conversion given a number of rows:
string convert(string s, int numRows);
思路
由于是从上到下再从下到上,我们可以使用一个string数组,记录zigzag之后每一行应该如何排列,按竖着来的方式将每个字符插入不同行数的string,最后将这个string数组结果拼接起来就可以了。
代码
class Solution {
public:
string convert(string s, int numRows) {
vector<string> zigzag(min(numRows,int(s.size())));
if ( numRows==1 ) // 注意不需要关心s的大小,只需要关心numRows大小
return s;
int currentRow = 0;
bool upsideDown = false;
for(char c:s){
zigzag[currentRow] += c;
if ( currentRow == 0 || currentRow == numRows-1 )
upsideDown = !upsideDown;
currentRow += upsideDown ? 1:-1;
}
string ret;
for(string s:zigzag){
ret += s;
}
return ret;
}
};
动态规划篇
746. 使用最小花费爬楼梯
描述
给你一个整数数组 cost ,其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用,即可选择向上爬一个或者两个台阶。
你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。
请你计算并返回达到楼梯顶部的最低花费。
示例 1:
输入:cost = [10,15,20]
输出:15
解释:你将从下标为 1 的台阶开始。
- 支付 15 ,向上爬两个台阶,到达楼梯顶部。
总花费为 15 。
示例 2:
输入:cost = [1,100,1,1,1,100,1,1,100,1]
输出:6
解释:你将从下标为 0 的台阶开始。
- 支付 1 ,向上爬两个台阶,到达下标为 2 的台阶。
- 支付 1 ,向上爬两个台阶,到达下标为 4 的台阶。
- 支付 1 ,向上爬两个台阶,到达下标为 6 的台阶。
- 支付 1 ,向上爬一个台阶,到达下标为 7 的台阶。
- 支付 1 ,向上爬两个台阶,到达下标为 9 的台阶。
- 支付 1 ,向上爬一个台阶,到达楼梯顶部。
总花费为 6 。
思路
首先我们能看出来,到达每个台阶所需要的费用只与它前两个台阶相关,则状态转移方程为:
fee[n] = min(fee[n-1] + cost[n-1], fee[n-2] + cost[n-2])其次我们发现我们可以随意选择前两个台阶开始,则:
fee[0] = 0; fee[1] = 0;初始量和状态转移方程都有了,则可以开始着手做题。
代码
class Solution {
public:
// fee[n] = min(cost[n-1] + fee[n-1], cost[n-2] + fee[n-2])
int minCostClimbingStairs(vector<int>& cost) {
if ( cost.size() < 2 ) {
return 0;
}
vector<int> fee(cost.size()+1);
// 可以选择从0级或者1级开始,说明到达0级或者1级的fee为0
fee[0] = 0;
fee[1] = 0;
for ( int n=2; n < fee.size();n++ ) {
fee[n] = min(cost[n-1] + fee[n-1], cost[n-2] + fee[n-2]);
}
return fee[fee.size()-1];
}
};198. 打家劫舍
描述
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
示例 1:
输入:[1,2,3,1]
输出:4
解释:偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。
示例 2:
输入:[2,7,9,3,1]
输出:12
解释:偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9),接着偷窃 5 号房屋 (金额 = 1)。
偷窃到的最高金额 = 2 + 9 + 1 = 12 。
思路
这个题目抽象出来的话,就是给定一个数组,每个整数可以选择取或者不取,如果第i个整数取,那么 第i-1或者i+1个整数就不能取。求怎么取数使得和最大。
从这里我们可以看出,实际上第i个取数和只与i-1, i-2个取数和相关,如果i-1取了,则第i取数和只能等于第i-1取数和(因为相邻,不能取了);或者i-1没取,当前第i取数和为i-2取数和加上nums[i]的和。
状态转移方程如下:
money[i] = max( money[i-1], money[i-2] + nums[i] )接下来我们找初始状态:
当i=0,只有第一个nums可以选,则
money[0] = nums[0]当i=1,则取第一个nums和第二个nums中更大的一个,则
money[1] = max(nums[0],nums[1])初始量和状态转移方程都有了,则可以开始着手做题。
代码
class Solution {
public:
// 数组中一个值被取了则另一个就不能取
// money[i] = max( money[i-1], money[i-2] + nums[i] )
int rob(vector<int>& nums) {
if ( nums.size() == 0 ) {
return 0;
}
if ( nums.size() == 1) {
return nums[0];
}
vector<int> money(nums.size());
money[0] = nums[0];
money[1] = max(nums[1],nums[0]);
for ( int i=2; i < money.size(); i++) { //注意n下标从2开始
money[i] = max( money[i-1], money[i-2] + nums[i] );
}
return money[money.size() -1];
}
};740. 删除并获得点数
描述
给你一个整数数组 nums ,你可以对它进行一些操作。
每次操作中,选择任意一个 nums[i] ,删除它并获得 nums[i] 的点数。之后,你必须删除 所有 等于 nums[i] - 1 和 nums[i] + 1 的元素。
开始你拥有 0 个点数。返回你能通过这些操作获得的最大点数。
示例 1:
输入:nums = [3,4,2]
输出:6
解释:
删除 4 获得 4 个点数,因此 3 也被删除。
之后,删除 2 获得 2 个点数。总共获得 6 个点数。
示例 2:
输入:nums = [2,2,3,3,3,4]
输出:9
解释:
删除 3 获得 3 个点数,接着要删除两个 2 和 4 。
之后,再次删除 3 获得 3 个点数,再次删除 3 获得 3 个点数。
总共获得 9 个点数。
思路
首先按nums[i]的大小把把其转换为一个count[]计数数组
count[i]表示在nums[]中,大小为i的数一共有几个
这样的话,删除 所有 等于 nums[i] - 1 和 nums[i] + 1 的元素
就转变为在count中,选了count[i]就不能选count[i-1]和count[i+1]
这道题就变为了打家劫舍的变体。
状态转移方程为:
credit[i] = max( credit[i-1], credit[i-2] + count[i] * i );初始状态为:
credit[0] = count[0];,credit[1] = max(count[0], count[1]);
53. 最大子数组和
描述
给你一个整数数组
nums,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。子数组 是数组中的一个连续部分。
示例 1:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4]
输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
示例 2:
输入:nums = [1]
输出:1
示例 3:
输入:nums = [5,4,-1,7,8]
输出:23
思路
我们可以用sum[i]代表以第 i 个数结尾的「连续子数组的最大和」(注意只是连续,而不是当前最大子数组和),这样的话最大值只要每次对比一下是否为最大值就行。
状态转移方程为:
sum[i] = max( sum[i-1] + nums[i], nums[i] );求最大值:
maxValue = max(maxValue, sum[i]);初始状态只有一个:
sum[0] = nums[0];
代码
class Solution {
public:
// sum[i]代表以第 i 个数结尾的「连续子数组的最大和」
// sum[i] = max( sum[i-1] + nums[i], nums[i] );
int maxSubArray(vector<int>& nums) {
vector<int> sum(nums.size());
sum[0] = nums[0];
int maxValue = -INT_MAX;
for ( int i=1; i< sum.size(); i++) {
sum[i] = max( sum[i-1]+nums[i], nums[i] );
maxValue = max(maxValue, sum[i]);
}
return maxValue;
}
};拓展篇
152. 乘积最大子数组
描述
给你一个整数数组 nums ,请你找出数组中乘积最大的非空连续子数组(该子数组中至少包含一个数字),并返回该子数组所对应的乘积。
测试用例的答案是一个 32-位 整数。
子数组 是数组的连续子序列。
示例 1:
输入: nums = [2,3,-2,4]
输出: 6
解释: 子数组 [2,3] 有最大乘积 6。
示例 2:
输入: nums = [-2,0,-1]
输出: 0
解释: 结果不能为 2, 因为 [-2,-1] 不是子数组。
思路
非动态规划,像是“最大子列和”的“在线处理”
首先假设存在某个最大乘积,然后对数组遍历,在经过每个元素的时候,有以下四种情况:
- 如果该元素为正数:
- 如果到上一个元素为止的最大乘积也是正数,那么直接乘上就好了,同样的最大乘积也会变得更大;
- 如果到上一个元素为止的最大乘积是负数,那么最大乘积会变成该元素本身,且连续性会被断掉;
(实际上无需考虑乘数为0的情况,因为对比是max(max_mul*nums[n],nums[n]),只要nums[0]为0那必然当前乘积为0)
- 如果该元素为负数:
- 如果到上一个元素为止的最小乘积也为负数,那么直接乘上就好了,此时最大乘积也会变得更大;
- 如果上一个元素为止的最小乘积为正数,那么最大乘积不会变,且连续性会被断掉;
我们同时需要保存最大乘积和最小乘积,因为最小乘积乘上一个负数可能会变得很大,最小值翻身变为最大值。
代码
class Solution {
public:
int maxProduct(vector<int>& nums) {
int res = -INT_MAX;
int max_mul = 1, min_mul=1;
for( int i=0; i<nums.size(); i++ ){
//当乘数nums[i]为负数的时候,此时乘上最小值(也为负数)才能得到最大值
if ( nums[i] < 0 ) swap(max_mul, min_mul);
max_mul = max( max_mul * nums[i], nums[i] );
min_mul = min( min_mul * nums[i], nums[i] );
res = max(max_mul, res);
}
return res;
}
};39. 组合总和
描述
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。
candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。
对于给定的输入,保证和为 target 的不同组合数少于 150 个。
示例 1:
输入:candidates = [2,3,6,7], target = 7
输出:[[2,2,3],[7]]
解释:
2 和 3 可以形成一组候选,2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选, 7 = 7 。
仅有这两种组合。
示例 2:
输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]
示例 3:
输入: candidates = [2], target = 1
输出: []
思路
使用回溯的想法。首先我们需要定好回溯结束条件,这题中我们需要多个组合,所以只需要target满足就往目标vector中添加元素就可以;之后需要确定如何遍历整个candidate,这里我们用一个for循环,但是要注意不要重复选择,所以for循环的i从加入候选routine里面的最后一个元素的index开始。
代码
class Solution {
public:
void dfs(vector<int> candidates, vector<vector<int>> &ans, vector<int> &path,int target, int begin){
if(target == 0){
ans.push_back(path);
return;
}
if(target<0){
return;
}
for ( int i=begin; i<candidates.size();i++ ){ // 注意i=begin,是传进来的参数,不然会每次都重复遍历
if(target - candidates[i] >=0){
path.push_back(candidates[i]);
dfs(candidates,ans,oneRout,target - candidates[i], i);// 注意传的还是i,因为每个元素可以重复利用
path.pop_back();
}
else {
break;
}
}
}
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
vector<vector<int>> ans;
vector<int> path;
sort(candidates.begin(),candidates.end()); //sort也需要注意,不然之后回溯有问题,如果没有sort则dfs里面for循环不需要if
dfs(ans,candidates,path,target,0);
return ans;
}
};3. 无重复字符的最长子串
描述
给定一个字符串
s,请你找出其中不含有重复字符的 最长子串 的长度。
示例 1:
输入: s = “abcabcbb”
输出: 3
解释: 因为无重复字符的最长子串是 “abc”,所以其长度为 3。
示例 2:
输入: s = “bbbbb”
输出: 1
解释: 因为无重复字符的最长子串是 “b”,所以其长度为 1。
思路
这里采用
unordered_set做为存储那个不重复字串st的数据结构,之后采用一个滑动窗口left~right。遍历字符串,每次到一个新的字符都判断unordered_set里面有没有与这个新字符相同的字符,有的话则从left开始,一个一个删除st[left]。
代码
class Solution {
public:
int lengthOfLongestSubstring(string s) {
unordered_set<char> st;
int count=0;
int left=0;
for(int right=0;right<s.size();right++){
while(st.find(s[right])!=st.end()){
st.erase(s[left]); // 注意删的是left
left++; // 注意是从左端开始,一个一个剔除,直到剔除掉那个重复的字符
}
count = max(count, right - left + 1);
st.insert(s[right]);
}
return count;
}
};本博客所有文章除特别声明外,均采用 CC BY-SA 3.0协议 。转载请注明出处!